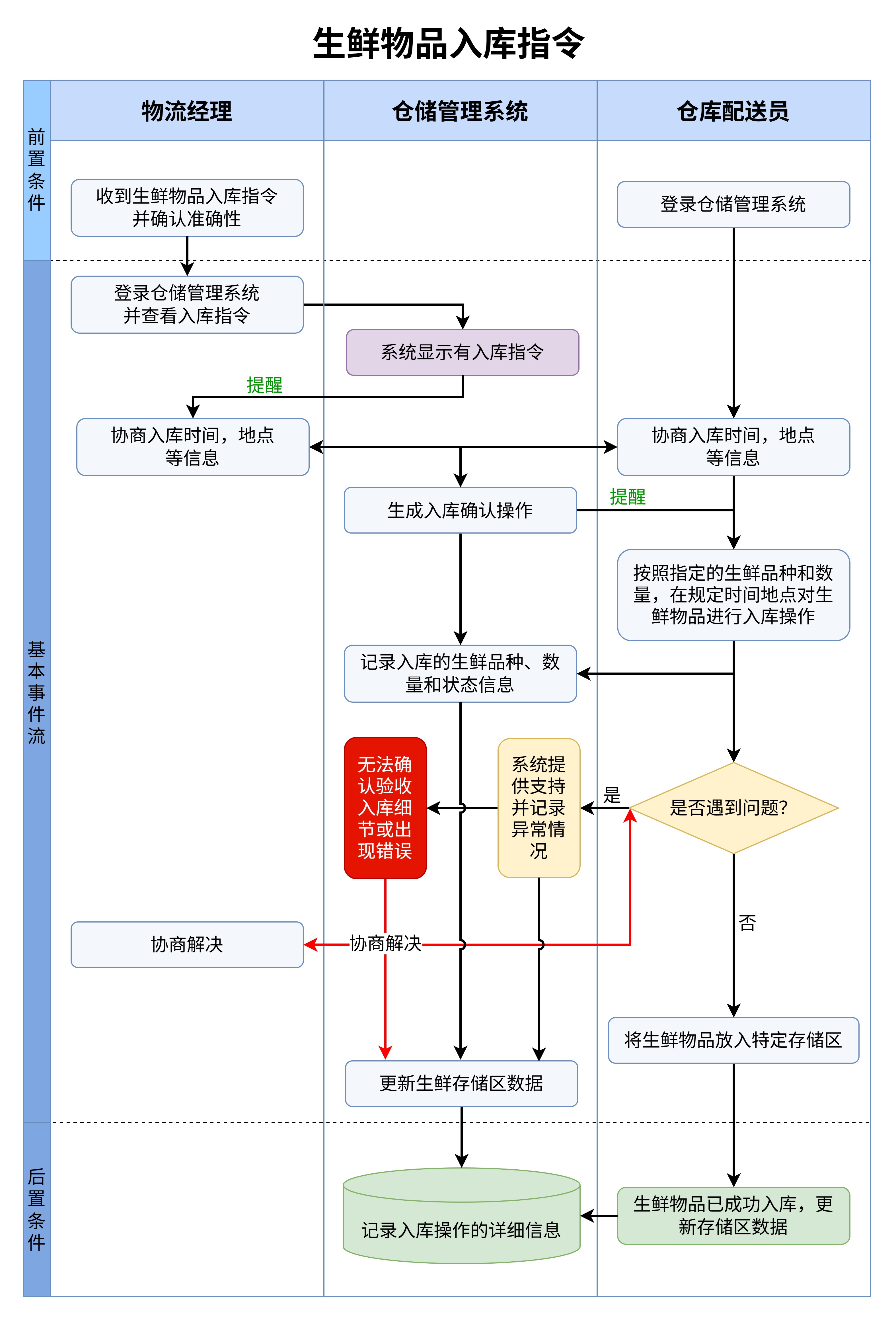
阶乘是数学中的一个基础概念,它不仅在理论上具有重要的地位,还在实际应用中起着至关重要的作用。大家可能听说过阶乘,但却不一定完全理解它的含义和计算方式。今天,我们将带您一起通过一个有趣的视角来了解1到10的阶乘之和,通过一张直观的流程图帮助您更好地掌握阶乘的概念。
我们来回顾一下阶乘的定义。阶乘(Factorial),通常表示为符号“!”后跟一个正整数,表示从1到该整数的所有正整数的乘积。例如,5的阶乘(5!)就是1×2×3×4×5。阶乘的计算规则如下:
阶乘看似简单,但它的增长速度却非常迅速。随着数字的增大,阶乘的值也呈指数级增长。因此,理解和掌握阶乘的计算,不仅能帮助我们解决很多数学问题,还能在实际生活中找到阶乘的应用。
我们来看看1到10的阶乘之和。列出1到10每个数的阶乘:
9!=1×2×3×4×5×6×7×8×9=362880
10!=1×2×3×4×5×6×7×8×9×10=3628800
1!+2!+3!+4!+5!+6!+7!+8!+9!+10!=1+2+6+24+120+720+5040+40320+362880+3628800=4037911
阶乘的计算虽然非常直接,但对于初学者来说,可能会感觉有些抽象和难以把握。因此,我们可以借助流程图来更好地理解这个概念。通过一张清晰的流程图,您可以一目了然地看到每一个阶乘的计算过程以及它们的叠加关系。
在这张流程图中,我们将每一个阶乘的计算过程分成了几个简单的步骤。从1开始计算1!,然后依次计算2!、3!、4!……直到10!,每一个步骤都将前一步的结果作为基础进行乘法运算。而阶乘之和的过程则是将每个计算结果逐一相加,最终得出总和。
通过这种方式,您不仅能理解阶乘的计算方法,还能更直观地感受到阶乘之和的递增趋势。这个流程图的作用在于,让复杂的阶乘计算过程变得简单、清晰,尤其对于那些刚接触阶乘概念的学生来说,帮助极大。
虽然阶乘在数学中占据着重要地位,但它的应用却远远超出了数学课本的范畴。阶乘在统计学、概率论、排列组合、计算机科学等领域都有广泛的应用。例如,在排列组合中,阶乘用来计算不同元素的排列顺序;在计算机科学中,阶乘被用来处理递归算法和动态规划问题。
了解1到10的阶乘之和,不仅帮助我们更好地掌握数学基础,还能为进一步深入学习其他高级数学概念打下坚实的基础。因此,掌握阶乘的计算方法,是每一位数学学习者必须经历的一项挑战。
阶乘的一个显著特点就是增长速度非常快。从1!到10!,我们可以看到数字迅速增大。实际上,阶乘的增长速度是超出大多数人想象的。10!的值已经达到3628800,而11!的值就直接跳跃到39916800。这个增速对很多实际问题来说是极其重要的,因为它涉及到很多涉及大数值的计算。
例如,在概率论中的组合问题,如果我们要求一个大集合的排列方式,阶乘便是必不可少的工具。随着元素的增加,阶乘会迅速让我们面对巨大的计算量。因此,掌握阶乘的基本规律和计算方法,对于解答这些问题至关重要。
除了排列组合,阶乘与其他数学公式也有着密切的关系。比如,在数学分析中,阶乘和无穷级数之间有着直接的联系。通过阶乘展开的泰勒级数,是求解函数近似值的重要工具。阶乘也和Γ函数(伽马函数)有着深厚的联系,Γ函数的定义扩展了阶乘的概念,使得它不仅可以用于整数,还可以用于实数和复数的计算。
通过了解阶乘的这些应用,您会发现,它不仅仅是一个简单的数学操作,更是一扇通向更广阔数学领域的门。
1到10的阶乘之和所代表的不仅仅是一个数字。它背后反映了数学的逻辑性与计算的美妙,给人一种探索数学奥秘的快感。通过阶乘,您可以看到数字背后蕴含的规律和深刻的数学思想。对于学生而言,掌握阶乘是向更高层次数学学习迈进的重要一步。
对于已经接触过更复杂数学概念的人,回顾1到10的阶乘之和,或许能帮助您重新审视数学的基础与美感。每一个阶乘的计算,都是数学思维的训练,都是解锁更复杂问题的钥匙。
所以,是否准备好通过阶乘的探索,发现更多数学世界的奇妙之处呢?这张1到10阶乘之和的流程图,或许正是您迈出数学探索第一步的完美工具。