良功绘图

更多免费模板

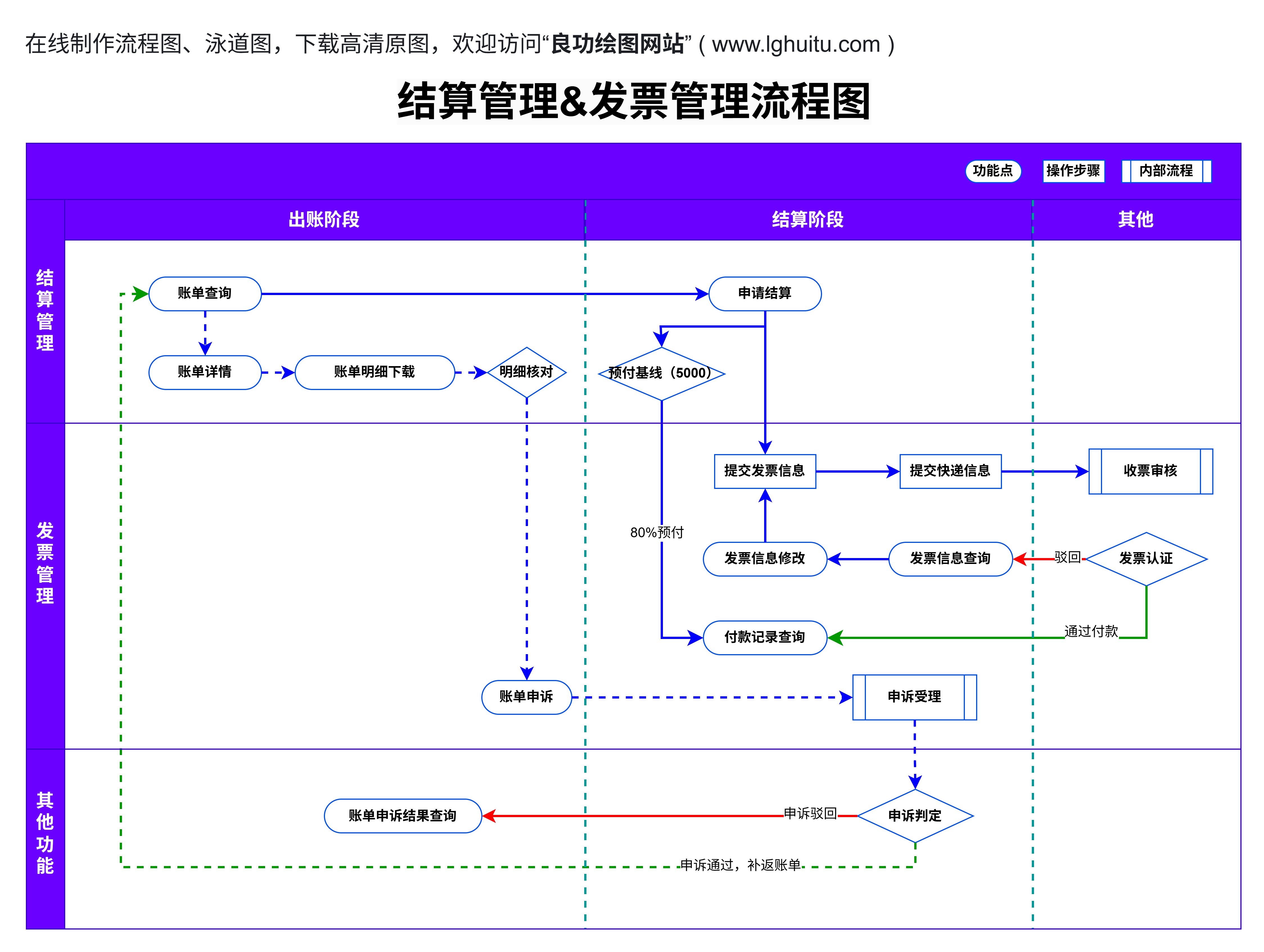
在数学领域中，阶乘是一个非常重要且常见的概念。它广泛应用于排列组合、概率统计、数论等多个领域。阶乘的计算方法看似简单，但在实际操作时，往往需要通过有效的算法和流程来帮助我们理清思路。今天，我们就以“5的阶乘的算法流程图”为主题，深入探讨其算法流程，让大家轻松掌握这一数学技巧。

什么是阶乘？

阶乘（Factorial）是一个正整数的乘积，它的定义是：对于一个正整数n，n的阶乘表示为n!，即从1到n所有整数的乘积。比如：

1!=1

2!=1*2=2

3!=1*2*3=6

4!=1*2*3*4=24

5!=1*2*3*4*5=120

可以看出，阶乘的计算就是一个累乘的过程，数字越大，计算量也就越大。因此，了解如何高效计算阶乘显得尤为重要。

5的阶乘（5!）计算过程

5的阶乘公式如下：

[5!=5\times4\times3\times2\times1=120]

这看起来似乎很简单，但如果我们要计算更大的阶乘，例如100!，就会发现普通的手工计算不仅繁琐，而且容易出错。因此，为了提高计算效率，我们通常会借助算法来实现阶乘的计算。我们将通过一个流程图来帮助大家理解5的阶乘的计算步骤。

阶乘的计算流程图

在计算5的阶乘时，可以使用递归算法或循环算法。无论是哪种方法，它们的核心思想都是逐步乘积，直到1为止。为了清晰地展示这一过程，我们通过一个简单的流程图来描述算法的执行过程：

开始：程序开始运行。

输入n的值：我们输入5这个值，表示我们要计算5的阶乘。

初始化结果变量：将结果初始化为1。

循环计算：从n到1逐个乘上当前数字，将每一步的乘积保存在结果变量中。

输出结果：最终输出计算结果120，即5的阶乘。

通过这种简单直观的方式，5的阶乘的计算变得清晰易懂。下面我们将详细分析如何实现这一流程，并探讨不同的算法实现方式。

循环法实现阶乘

循环法是一种常见的阶乘计算方式。其思想就是从1开始累乘，一直到n。具体来说，计算5!的过程可以分为以下几个步骤：

初始化结果变量为1。

从1循环到5，每次将当前的数字与结果变量相乘。

最终得到的结果即为5的阶乘。

以下是循环法的伪代码示例：

result=1

foriinrange(1,6):

result*=i

print(result)#输出120

递归法实现阶乘

除了循环法，递归法也是计算阶乘的一种常见方法。递归的思想是将一个大问题分解成若干个小问题来解决，直到问题简化为最基本的情况。在阶乘的计算中，递归的基本公式是：

[n!=n\times(n-1)!]

递归的终止条件是当n等于1时，返回1。基于此，我们可以通过递归函数来计算5的阶乘。以下是递归法的伪代码示例：

deffactorial(n):

ifn==1:

return1

else:

returnn*factorial(n-1)

print(factorial(5))#输出120

流程图在算法中的应用

流程图是描述算法执行过程的一种图形化方法，它能帮助我们更直观地理解算法的执行逻辑。在计算阶乘时，流程图能够清晰地展示出每一个步骤，避免了复杂的文字描述和理解上的难度。

以5的阶乘为例，流程图可以帮助我们迅速把握算法的结构。在实际的编程开发中，尤其是当算法较为复杂时，使用流程图可以帮助开发人员更好地理清思路，减少实现过程中的错误。

为什么要使用算法流程图？

使用算法流程图有以下几个显著的优势：

直观易懂：对于初学者来说，流程图能够直观地展示出算法的执行步骤，帮助理解每一步的计算逻辑。

降低错误率：在编程过程中，流程图能帮助开发者理清思路，避免遗漏步骤或出错。

提高效率：通过流程图的引导，开发者能够更快速地实现算法，特别是在面对复杂算法时，流程图能够起到事半功倍的效果。

无论是在学习阶段还是在实际的编程开发过程中，算法流程图都能起到不可替代的作用，它帮助我们将抽象的计算过程变得具体、清晰。

阶乘算法在实际中的应用

虽然阶乘看起来只是一个简单的数学概念，但它在许多实际问题中都有着广泛的应用。例如，在概率论和统计学中，阶乘被用于排列和组合的计算。无论是做概率题目、研究数学模型，还是进行数据分析，阶乘算法都能提供强大的数学支持。

而随着现代计算机技术的发展，阶乘算法也得到了更加高效的实现方式。例如，在大数据计算和科学计算中，算法的优化和高效执行至关重要。借助计算机的高速运算能力，阶乘的计算可以在毫秒级别完成，极大地提高了效率。

阶乘算法不仅限于5!的计算，它的原理和应用贯穿了整个数学和计算科学的领域。在本文的第二部分，我们将继续探讨5的阶乘的算法流程图的进一步应用，如何在实际问题中利用这一算法，并通过改进算法优化效率。

阶乘在组合数学中的应用

组合数学是数学的一个重要分支，涉及到各种计数问题。在解决排列和组合问题时，阶乘的计算是一个基础且关键的工具。比如，在排列组合公式中，阶乘往往用于计算不同排列的个数。一个常见的排列组合问题是从n个物体中选择r个物体，且顺序不同，这时可以用到阶乘来计算。

排列数公式为：

[

P(n,r)=\frac{n!}{(n-r)!}

]

而组合数公式则是：

[

C(n,r)=\frac{n!}{r!(n-r)!}

]

通过这些公式，我们可以利用阶乘计算排列和组合的结果。在实际应用中，例如在彩票选号、排列问题等领域，阶乘的计算显得尤为重要。

阶乘在计算机科学中的应用

除了在数学领域中的广泛应用外，阶乘算法还广泛应用于计算机科学和编程中。例如，在一些算法设计和数据处理过程中，阶乘被用来计算不同的可能性或不同的排列方式。特别是在图论和网络算法中，阶乘常常用于表示路径的选择数目。

在计算机图形学、人工智能等领域，阶乘也被用于图像处理、机器学习模型的优化等计算任务中。在这些任务中，如何高效地计算大数阶乘成为了一个挑战。通过优化算法，例如动态规划、缓存技术等，阶乘的计算能够大幅度提高计算速度，从而提高整体系统的性能。

优化阶乘算法

尽管递归和循环算法是阶乘计算的基本方法，但当阶乘数值变得很大时，直接计算可能会导致溢出或性能低下。因此，在实际应用中，我们需要对阶乘算法进行优化。

一种常见的优化方法是使用动态规划。通过缓存中间结果，可以避免重复计算，从而提高算法的效率。例如，我们可以通过存储已计算的阶乘值，在计算更大阶乘时直接查找缓存，避免重复计算。

对于非常大的阶乘，我们还可以使用对数技巧来避免直接计算大数。通过将阶乘转换为对数形式，可以减少计算的复杂度。

总结

5的阶乘作为一个基础的数学概念，不仅在学术研究中有着重要作用，也在实际生活和工作中得到广泛应用。通过掌握5的阶乘的算法流程图和不同的算法实现，我们可以更高效地解决数学计算问题。无论是在学术研究、编程开发，还是在实际的工程问题中，了解阶乘算法的基本原理和优化技巧，都会为我们带来更高效的解决方案。