在学习数学的过程中,我们经常会遇到一个重要的概念——阶乘。阶乘是指从1乘到指定数字的所有整数的积,是数学中极为基础却又充满魅力的一个概念。对于许多人来说,阶乘的计算可能看似复杂,但实际上,如果能够掌握它的计算规则及流程,便能轻松应对这一问题。
我们常常会用符号“n!”来表示一个数字n的阶乘,其中n是正整数。例如,5的阶乘就是5!,它表示从1到5所有整数的乘积,也就是:
看起来虽然简单,但如何将这个计算过程更加清晰地呈现出来呢?在这篇文章中,我们将通过5的阶乘算法流程图来帮助你更直观地理解阶乘的计算过程。
在讨论5的阶乘之前,我们需要了解阶乘的一些基础概念。阶乘是数学中的一种基本运算,表示从1乘到指定数字的所有整数的积。对于任意一个正整数n,n的阶乘表示为n!。例如,5!就是5的阶乘,等于:
阶乘在许多数学公式中都有广泛应用,尤其是在组合数学、排列组合、概率论以及计算机科学等领域中,阶乘经常作为重要的计算基础出现。
阶乘的一个重要特点是递归性。例如,n的阶乘可以通过n-1的阶乘来递归地计算,具体来说就是:
而1!则被定义为1,0!的值被定义为1,这样能够确保递归公式的正确性。
要计算5的阶乘,理解整个计算过程是非常重要的。虽然阶乘的计算方法比较简单,但如果通过流程图的形式来呈现,可以帮助你更加清晰地理解每一步的操作。这种视觉化的呈现方式,不仅有助于加深对概念的理解,还能帮助你在解决更复杂的数学问题时,理清思路,迅速找到正确的答案。
我们将通过一个简单的流程图,详细展示5的阶乘计算过程。你将看到,在计算过程中,如何从数字5开始,逐步递减并进行乘法运算,最终得出结果。
一个有趣的地方是,阶乘不仅可以通过直接乘法计算,还可以通过递归的方式进行计算。递归计算就是将一个问题转化为更简单的子问题来解决。例如,5的阶乘可以通过以下的递归公式来表示:
每个阶乘都可以通过递归计算,而1!和0!的定义确保了递归能够顺利结束。
这种递归方式可以让你更好地理解阶乘的深层次结构,掌握递归思想的应用。
在上面,我们简单介绍了如何计算5的阶乘,并且给出了详细的计算步骤。我们将通过具体的流程图来更直观地呈现这个过程,帮助你更好地理解5的阶乘算法。
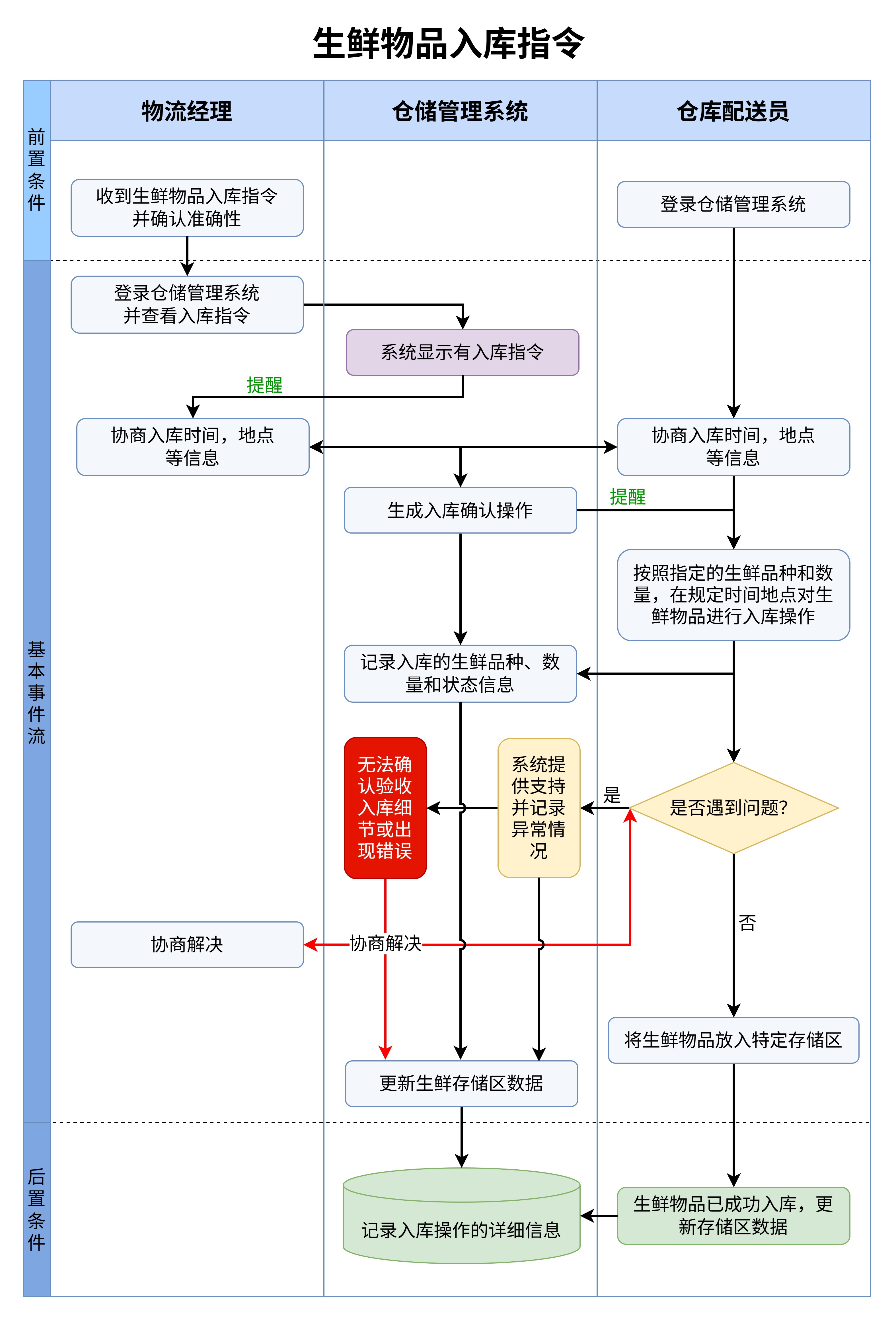
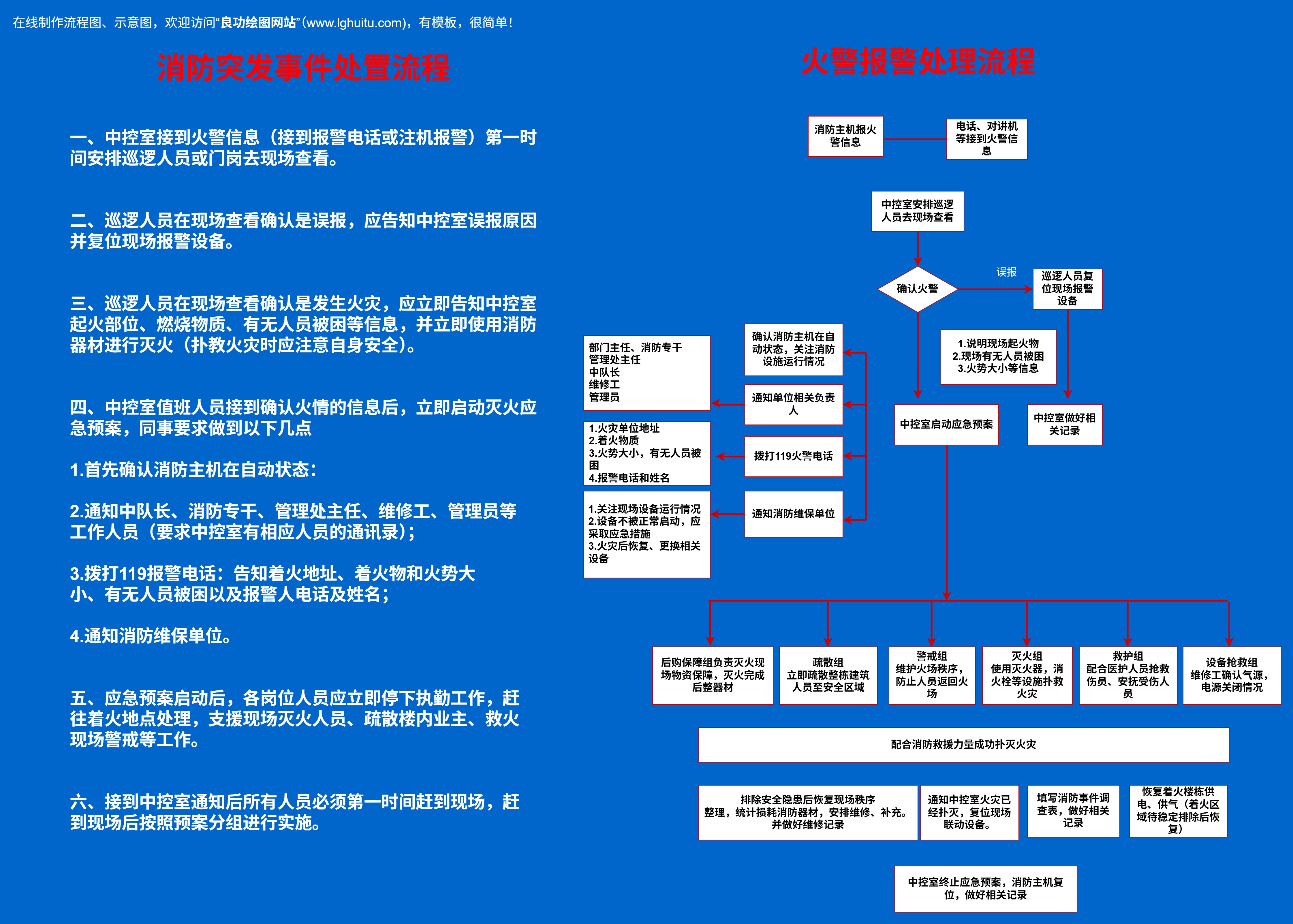
想象一下,你面前有一张图表,这张图清晰地列出了从开始到结束的每个步骤,展示了如何从数字5计算到5!的结果。流程图的核心是将每个步骤拆解成简单的操作,每一步都可以清晰地看到从一个状态到另一个状态的转变。通过这种方式,你能够在理解计算过程的感受到阶乘计算背后的逻辑。
流程图的每个步骤都包含了一个简单的操作,比如从数字5开始,依次与4、3、2、1相乘,直到最后得出结果。这些步骤的逻辑关系通过箭头连接,形成一个连贯的流程。
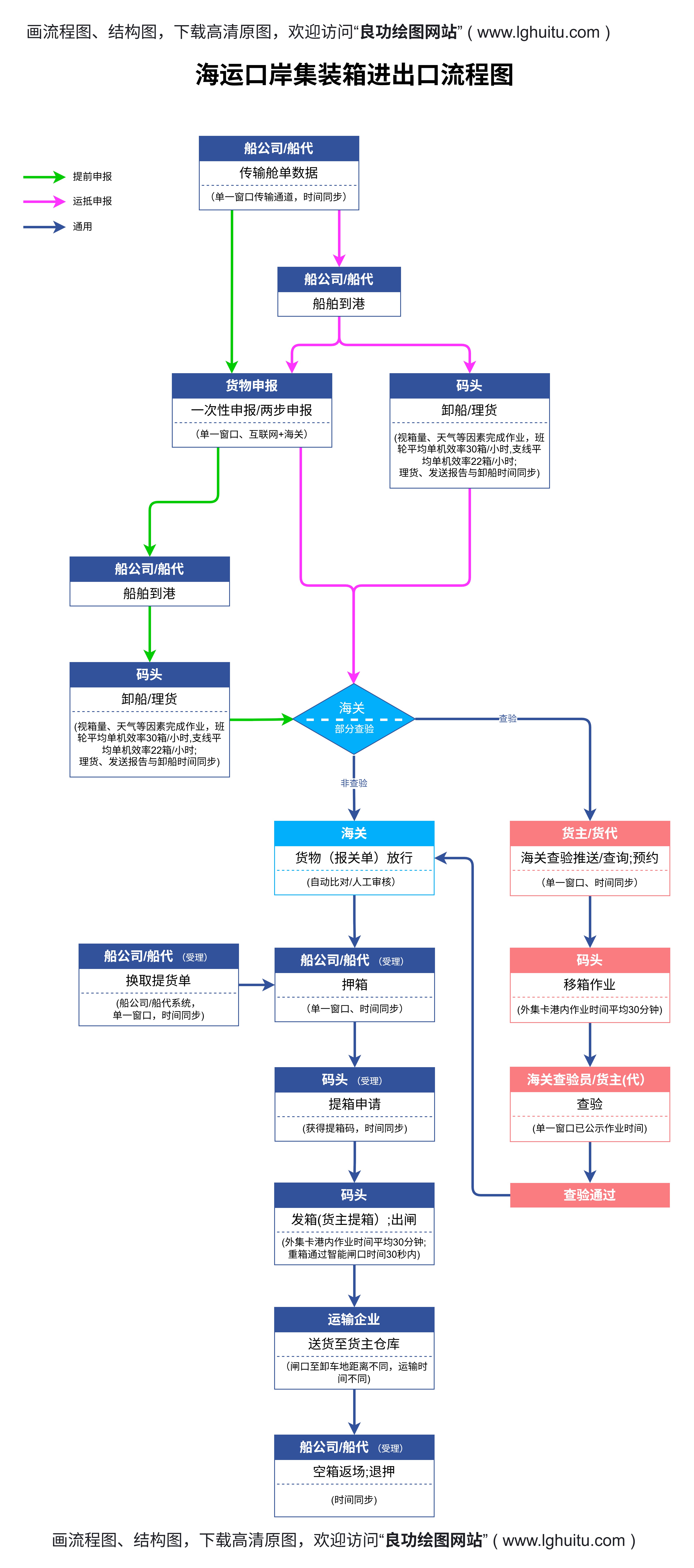
流程图的设计主要是将5的阶乘计算过程以图形的方式呈现出来。在流程图的最顶部,我们从5开始,然后依次连接到下一个操作,每个操作的结果都会显示在图中的箭头旁边。例如,第一个步骤是5×4,结果是20;接着,20×3,结果是60;然后是60×2,结果是120;最后是120×1,得出最终结果120。
通过这种设计,流程图不仅使计算过程变得更加直观,而且能够帮助学生或初学者清晰地看到每一个步骤的操作。通过这种图形化的方式,学习者可以更快地掌握阶乘的计算方法。
通过使用流程图,学生可以以一种更直观的方式掌握复杂的数学运算,尤其是阶乘这样的基础概念。与传统的文字描述不同,流程图能够帮助学生将复杂的步骤简化为一个个清晰的操作节点,使得每个细节都不被忽视。这样的视觉化学习方式,不仅让学习者更加容易理解抽象的数学概念,而且能够帮助他们在今后的数学学习中,更好地解决类似的问题。
5的阶乘虽然看似简单,但它背后的算法和计算方法却充满了深刻的数学原理。通过流程图的帮助,我们能够将这个过程拆解成每一个细节,进一步加深对阶乘的理解。无论是在数学学习还是实际应用中,掌握阶乘的计算方法都是非常重要的,它不仅是解决其他数学问题的基础,也是理解更高阶数学知识的重要步骤。
如果你对5的阶乘算法流程图感兴趣,不妨动手尝试绘制一个自己的流程图,让数学变得更加有趣,深入理解其中的奥秘。