在学习数学的过程中,阶乘(Factorial)这一概念常常成为我们遇到的基础问题之一。无论是做数学题,还是进行编程实践,阶乘的计算都无处不在。而其中的5!(5的阶乘)作为一个典型例子,它不仅仅是一个数学问题,更是了解算法和计算思维的一个绝佳切入点。今天,我们就以5!的计算为例,来解密这一基本概念,并通过流程图让你更直观地了解其背后的计算流程。
我们来回顾一下阶乘的定义。阶乘是指一个正整数n的阶乘,记作n!,是指从1到n所有整数的连乘积。例如,5!表示从1乘到5的结果。公式如下:
5!=5\times4\times3\times2\times1=120
简而言之,5!的计算过程就是将1至5的数字依次相乘,最终得到120这个结果。虽然这个过程在数字较小的时候看起来并不复杂,但在计算机科学和编程中,阶乘的计算方式却有着深远的意义。
阶乘不仅仅是数学中一个简单的运算,它在许多算法和应用中起着重要作用。例如,在组合数学中,阶乘常用来计算排列和组合问题;在概率论中,阶乘也频繁出现在计算各种事件概率的公式中。而在计算机科学中,阶乘的递归计算方式成为许多程序设计问题的经典范例。
举个例子,如果你要计算从一群n个元素中选出r个的不同排列方式,可以使用排列公式:
阶乘的应用广泛而深入,因此理解其背后的计算原理,对于任何一个学习编程和算法的学生来说,都是一个必不可少的基础。
为了让大家更清晰地理解5!的计算过程,我们将通过流程图来展示整个计算过程。通过流程图,我们不仅能明确每一步的操作,还能清楚地看到每个步骤的输入和输出。下面是5!阶乘计算的流程图。
从流程图中,我们可以看到5!的计算步骤是怎样逐一展开的。我们从1开始,将它与5相乘,然后继续与4、3、2、1依次相乘,直到最后得出120这个结果。这个计算过程简单但却展示了一个基本的递归思想:每一步的结果都依赖于前一步的结果,直到最终得出完整的计算结果。
通过上述的流程图,我们不仅能直观地看到计算过程,还能理解其中所蕴含的算法思想。这个算法非常适合用递归方式进行实现。递归是一种常见的编程技术,它通过调用自身来解决问题。在计算阶乘时,递归的思路通常是将n!拆分成n×(n-1)!,直到n为1为止,这样就可以逐步完成阶乘的计算。
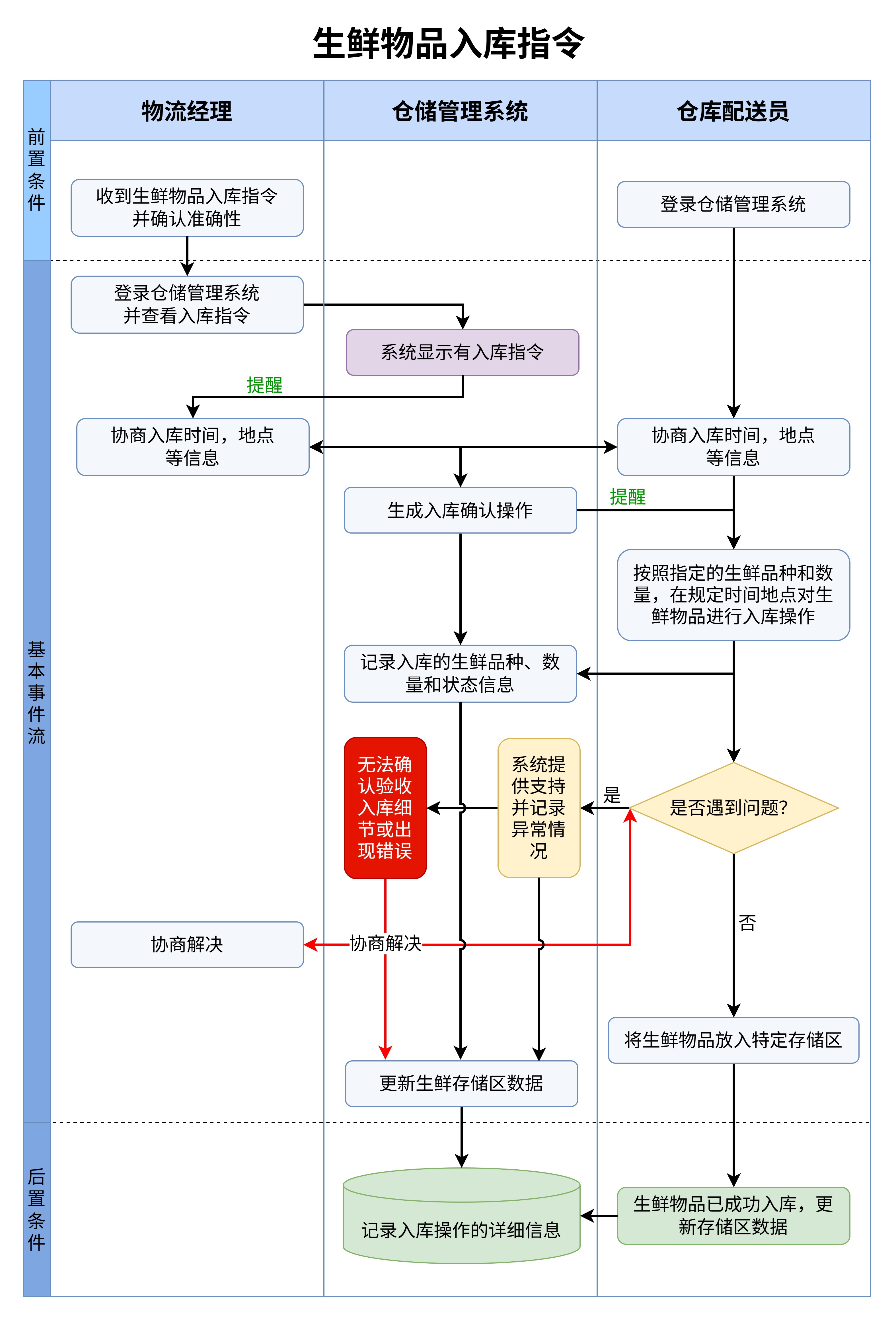
5!=5\times(4\times(3\times(2\times(1!))))
通过递归调用,程序会不断地将计算任务分解,直到最终达到基本情况1!=1,从而顺利返回计算结果。这种分解问题的思维方式,是很多高级算法的基础,也是我们在编程时经常使用的一种技巧。
我们已经提到过,5!的计算可以通过递归来实现,但事实上,还有另一种常见的方法——迭代。递归和迭代这两种方法虽然在本质上都能解决问题,但它们在实现和效率上各有优缺点。
递归的方式可以很好地模拟数学上阶乘的定义,而且它在代码实现上通常较为简洁。递归代码的结构通常是简明的,容易理解。不过,递归方式在处理大数阶乘时可能会面临栈溢出的风险,因为每次递归调用都会占用栈空间。当n值非常大时,递归深度会变得很深,这可能导致程序的内存消耗过大,甚至出现程序崩溃。
相比之下,迭代的方法则不会面临递归深度过大的问题。迭代通过循环的方式一步步计算阶乘,避免了栈溢出的风险。在处理大数据量时,迭代通常比递归更加高效。迭代的缺点是代码可能会稍显复杂,但它在许多情况下仍然是一个优选方案。
举个例子,5!的递归实现与迭代实现的代码对比如下:
deffactorial_recursive(n):
returnn*factorial_recursive(n-1)
deffactorial_iterative(n):
通过这两种实现方式,我们可以看到,递归实现非常简洁,符合数学定义,而迭代实现则更加直接,且能避免栈溢出的风险。
阶乘计算的递归与迭代方法在实际编程中都有应用。很多编程语言都提供了内置的阶乘函数,帮助开发者更高效地完成这一任务。理解其背后的计算原理,尤其是递归与迭代的区别,对于程序员来说至关重要。掌握这些基本的算法思想,可以帮助我们在面对更复杂的算法时,能够灵活运用不同的技巧和方法。
通过今天的学习,我们不仅理解了5!阶乘的计算过程,还通过流程图更清晰地掌握了计算的每一步。我们还探讨了递归与迭代两种计算方法的优缺点。在编程和算法设计中,阶乘的计算是一个基础而重要的概念,它帮助我们更好地理解递归与迭代两种算法思想的应用。
无论你是刚接触编程的初学者,还是已经有一定经验的开发者,理解和掌握这些基础的算法思想,都是你迈向更高水平的必经之路。希望本文能够帮助你深入理解5!阶乘的计算流程,并激发你对算法的兴趣,探索更多精彩的数学和编程世界。