在数学的世界里,阶乘是一个极其重要的概念,它常常出现在排列组合的计算中。对于一个正整数n,阶乘(n!)表示的是从1乘到n的所有整数的积。看似简单的数学公式,却常常让学生在理解时感到困惑,特别是在计算复杂的阶乘时。为了帮助大家更好地理解这一概念,本文将通过流程图的方式来形象展示n!的计算过程。
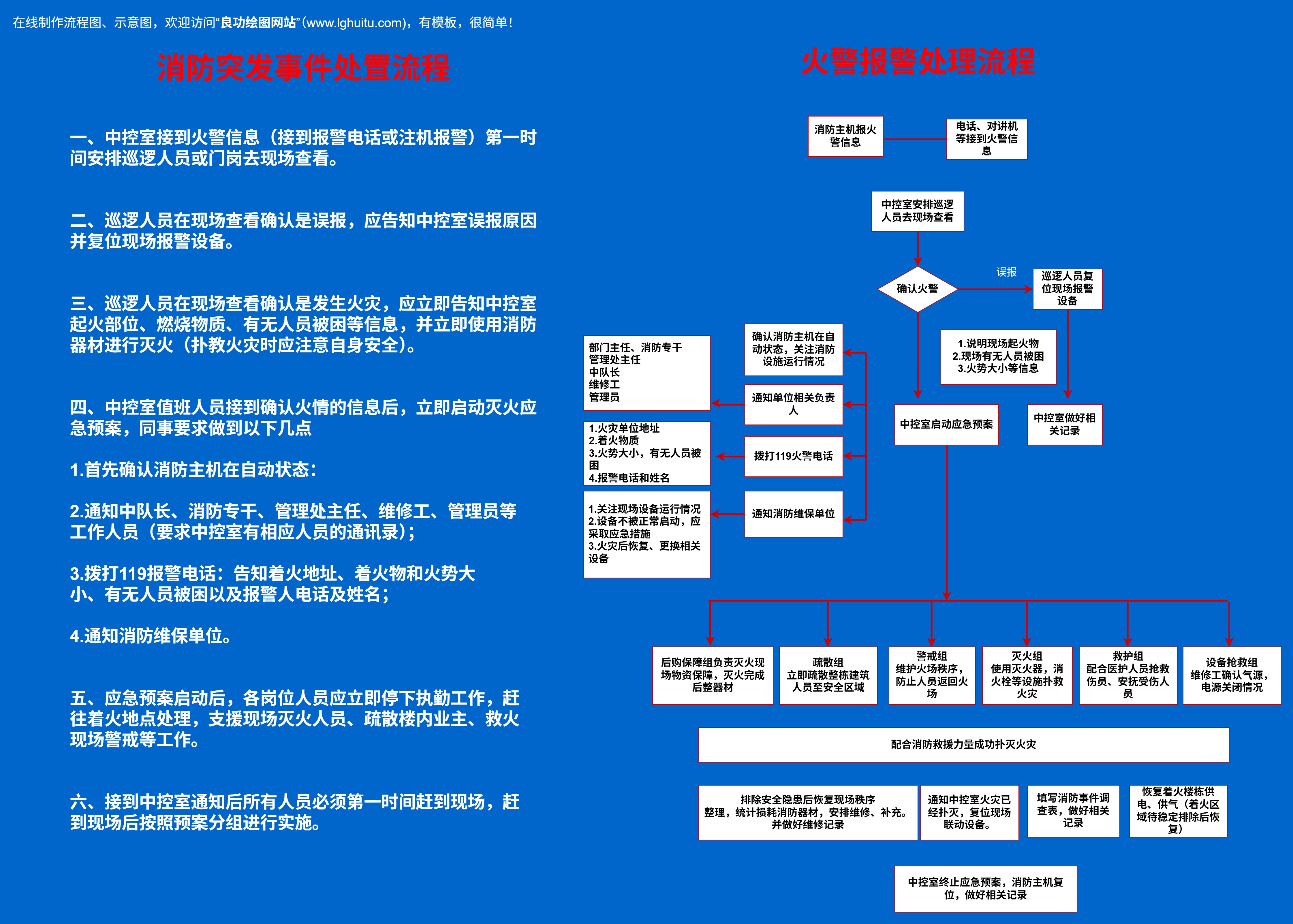
让我们从阶乘的定义开始。在数学中,n!(读作“n的阶乘”)的定义如下:
例如,5!的计算过程是:5!=5×4×3×2×1=120。
阶乘的计算并不总是那么简单,尤其是当n的值非常大的时候,手动计算变得非常繁琐。为了让这一过程变得更加清晰,我们可以通过流程图来一步步展示这个计算过程。
在流程图中,我们将n!的计算过程分为几个步骤。流程图的起始点是n的值。然后,我们通过判断n是否大于1来决定接下来的操作。如果n小于等于1,则阶乘的结果为1,这是阶乘的基础定义(例如0!=1,1!=1)。如果n大于1,我们将n与n-1的阶乘结果相乘,直到n减到1为止。
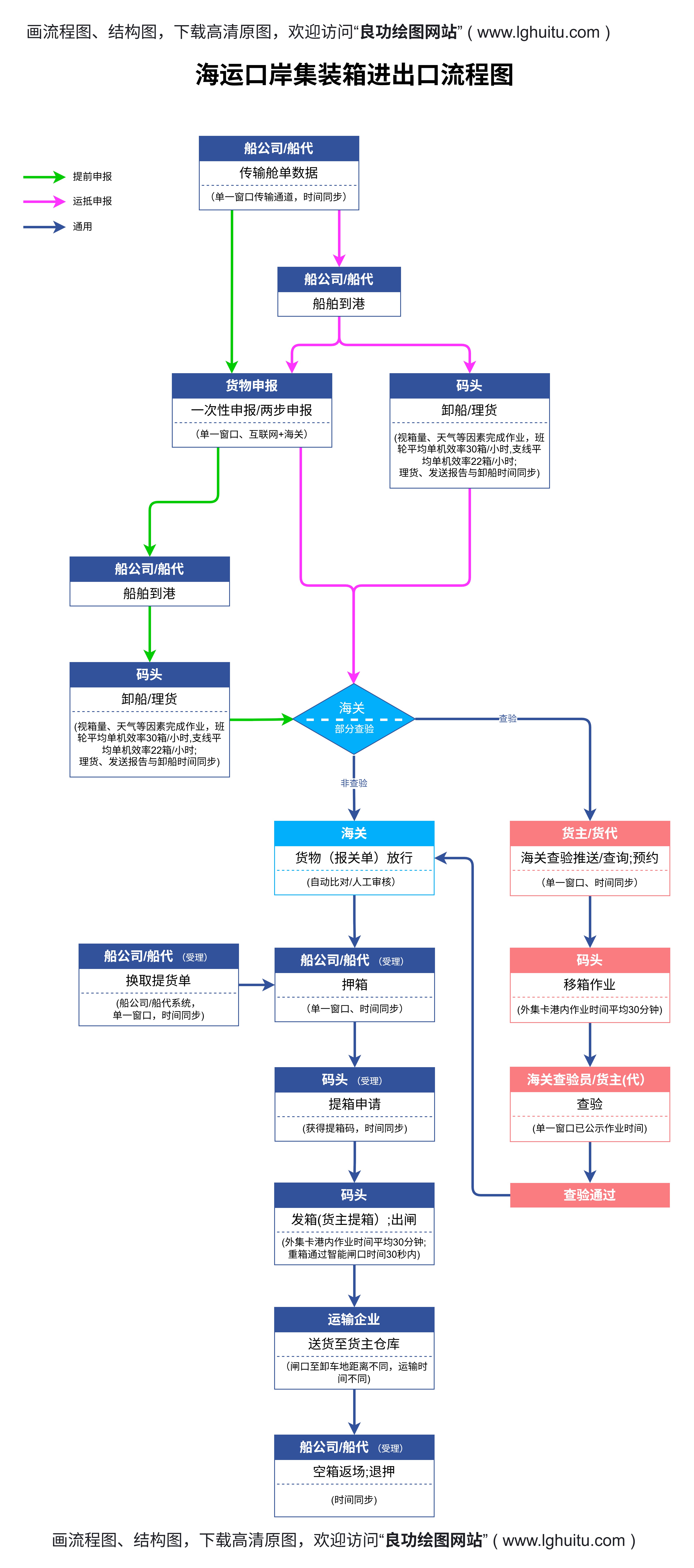
这个计算过程可以通过一个简单的流程图来表示。流程图的每一个步骤都清晰地展示了计算过程的逻辑。例如,从n开始,逐步进入下一个步骤,每次将n与n-1的结果相乘,直到所有的乘法操作完成为止。最终,我们将得到n!的值。
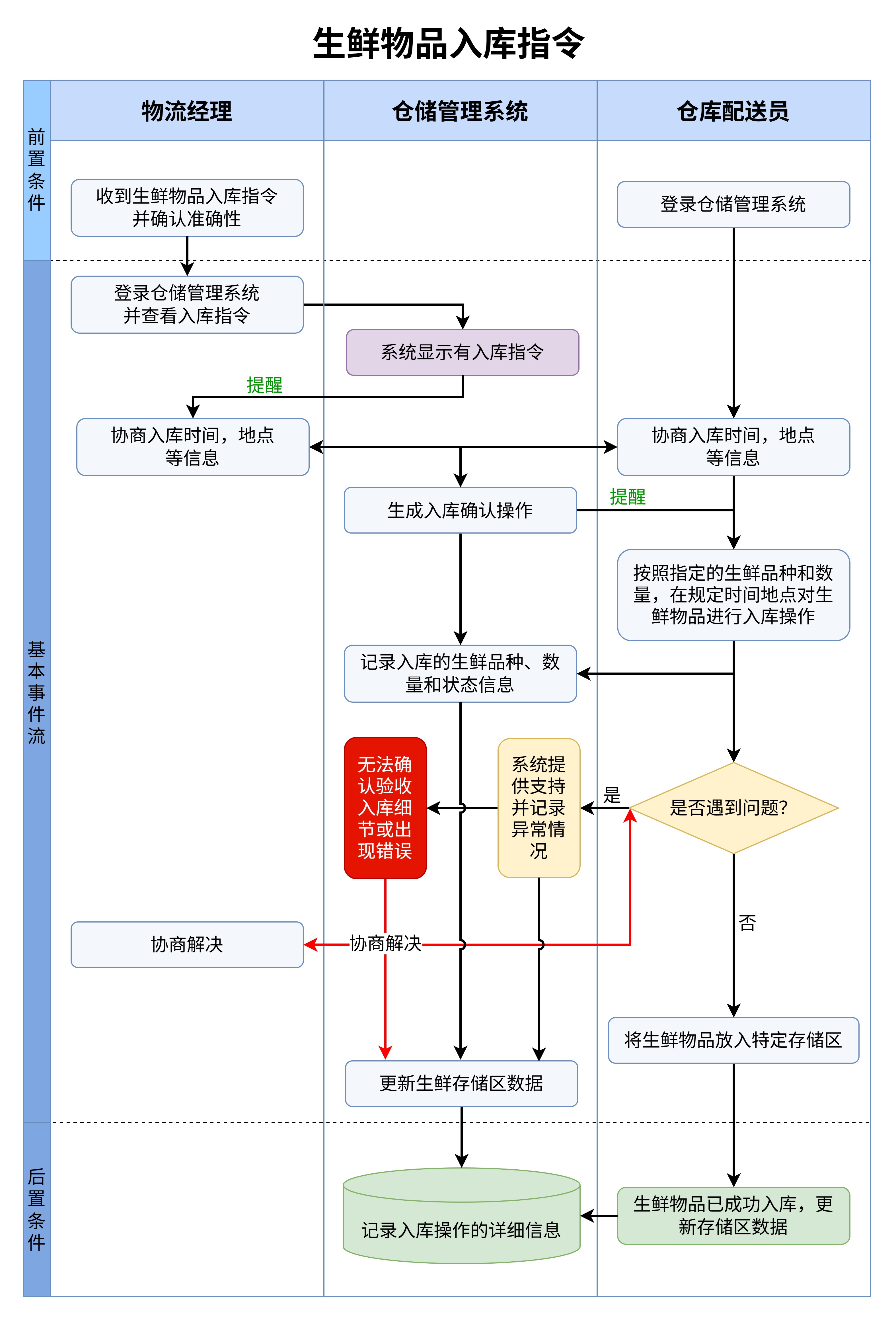
通过这种方式,流程图不仅能够让我们直观地看到每一步的操作,还能帮助我们理解阶乘的递归性质。递归是指在计算n!时,n!的值是通过计算(n-1)!再乘以n得到的。这样一来,n!的计算过程就变得更加清晰可见。
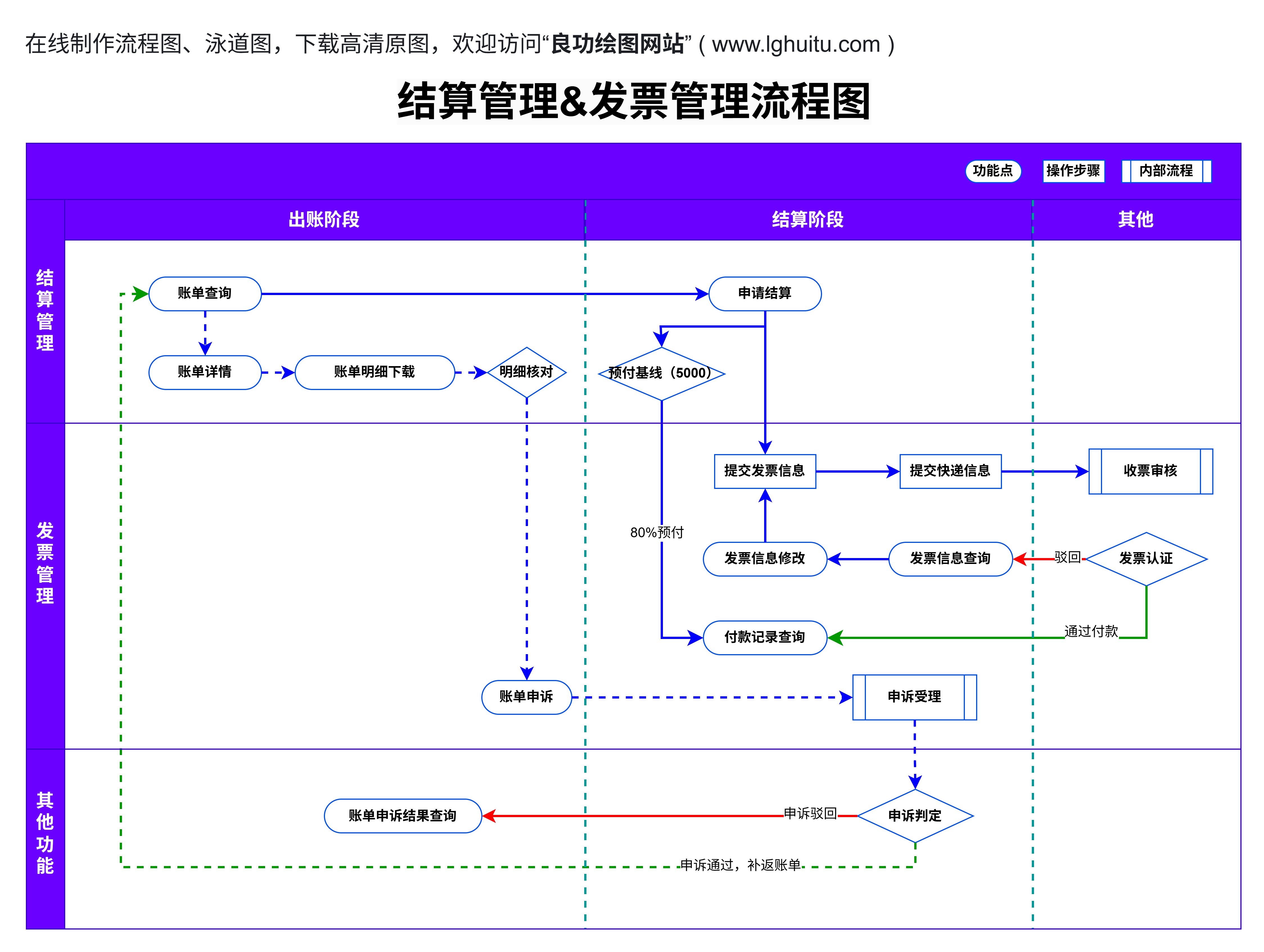
通过引入流程图,我们不仅可以帮助学生更好地理解阶乘的计算过程,还能让他们在学习过程中更加专注于每一步的推导,而不是陷入繁琐的计算细节中。这样,学习数学变得更加生动、有趣,也让抽象的概念变得更加易于掌握。
除了在课堂上使用,流程图的方式也适用于数学考试的准备。当你面对复杂的排列组合问题时,通过绘制流程图,可以帮助你清晰地梳理每一步的计算步骤。这样,不仅能提高解题效率,还能减少因计算错误而导致的失误。通过这种方式,数学学习不再是一项枯燥的任务,而是充满了逻辑和条理的思维过程。
在接下来的部分中,我们将继续通过具体的例子来进一步探讨如何利用流程图简化阶乘计算的过程,并展示其在实际应用中的重要性。
在上文中,我们介绍了阶乘的基本概念以及如何利用流程图来展示n!的计算过程。在实际应用中,如何通过流程图来更好地应用这一概念呢?
阶乘在排列组合问题中扮演着极其重要的角色。例如,假设我们有5个不同的物品,想要将它们排成一行。根据排列公式,排列数就是5!,也就是5×4×3×2×1=120。通过流程图的方式来表示这个计算过程,不仅能够帮助我们理解排列的基本原理,还能帮助我们更高效地进行计算。
在这种情况下,流程图的作用就非常明显了。我们可以将5个物品标记为A、B、C、D、E。接着,按照流程图的指引,我们可以依次计算每一步的乘法操作,最终得到排列数120。通过这种方式,学生可以将复杂的排列组合问题转化为一系列简单的乘法计算,从而轻松求解问题。
阶乘的概念还广泛应用于概率论中。在概率论中,很多问题都涉及到从一组元素中选择若干个元素进行排列或组合,这时候就需要使用阶乘来进行计算。通过流程图,我们可以清晰地看到每一个排列或组合的步骤,帮助我们更好地理解概率的计算方法。
例如,在一个包含10个不同号码球的抽奖箱中,抽取5个球进行排列。这个问题的解答就涉及到10!与5!的计算。通过绘制流程图,我们可以将整个过程逐步分解成简单的步骤,帮助我们准确地进行计算,避免因为遗漏某个步骤而导致的错误。
流程图还可以帮助我们在解决更为复杂的数学问题时,理清思路、简化操作。例如,在一些复杂的数列和级数问题中,阶乘作为数列的关键部分,往往需要通过多次递归计算来求解。这时,通过绘制清晰的流程图,我们可以逐步跟踪每一个计算过程,确保每一步都没有错误。
利用流程图来表示n!的计算过程,不仅可以帮助我们更加直观地理解阶乘的计算方法,还能提升我们解决问题的效率。通过流程图的展示,数学学习不再是一件枯燥的事情,而是充满了逻辑和美感的思维过程。无论是在课堂学习、考试准备,还是在实际应用中,流程图都是帮助我们理解和运用阶乘这一数学概念的重要工具。
通过不断实践,我们将发现,流程图不仅仅是一个简单的绘图工具,它还能帮助我们更深入地理解数学原理,提升我们解决实际问题的能力。而阶乘的计算,也在这样一种清晰而直观的方式中变得简单易懂,成为数学世界中一个不可或缺的基本工具。