良功绘图

更多免费模板

在数学的世界里，有很多看似简单却充满魅力的概念，而阶乘就是其中之一。阶乘的计算不仅是数学基础中的一项重要内容，也是程序设计中常常需要用到的一种操作。今天，我们将深入探讨一个具体的例子——计算并输出5的阶乘，并通过流程图来展示这一过程。无论你是数学爱好者，还是学习编程的小白，这篇文章都会让你对阶乘有一个更清晰、更深刻的理解。

什么是阶乘？

阶乘是数学中非常基础且重要的一个概念，通常用符号“!”表示。对于一个自然数n，n的阶乘是指所有小于等于n的正整数的积。例如，5的阶乘用符号5!表示，计算过程为：

[

5!=5\times4\times3\times2\times1=120

]

可以看出，阶乘的计算是一个递归的过程。它不仅仅限于整数5，任何正整数的阶乘都可以通过这种递归的方式来求解。

5的阶乘计算过程

我们以5的阶乘为例，来详细讲解这一计算过程。计算5的阶乘可以分为以下几个步骤：

初始化：我们从数字5开始。

乘积计算：依次将数字5、4、3、2和1相乘。

输出结果：将所有数相乘的结果输出，得到最终的阶乘值120。

这些步骤可以通过图形化的流程图来直观展示。通过流程图，我们可以清晰地看到计算5的阶乘时的每个具体步骤，从而帮助我们更好地理解这一过程。

阶乘的递归性质

在计算5的阶乘时，我们其实使用了一个递归的思想。在编程中，递归是一种非常常见的算法设计技巧。5的阶乘可以分解为5乘以4的阶乘，而4的阶乘又可以分解为4乘以3的阶乘，依此类推，直到乘到1为止。这个递归过程本质上是一个不断将问题拆解成更小子问题的过程。

这种递归的计算方式在编程中有着广泛的应用。例如，在编写计算阶乘的程序时，我们可以通过递归函数来实现。这种方法不仅能够简化代码，还能帮助我们更好地理解和运用递归的思想。

5的阶乘的实际应用

阶乘在数学中有着广泛的应用，尤其是在组合数学、概率论以及计算机科学中。在计算排列组合问题时，阶乘的概念是不可或缺的。例如，在排列问题中，我们需要计算从n个不同的物品中选出r个物品进行排列的总数，这时就需要用到阶乘的运算。

除此之外，阶乘在计算机科学中的应用也非常广泛。无论是在编写算法、分析时间复杂度，还是在计算数据的排列组合时，阶乘都是必不可少的工具。随着我们对阶乘概念的深入理解，我们会发现，它在各个学科中的重要性远超我们的想象。

用流程图展示5的阶乘计算过程

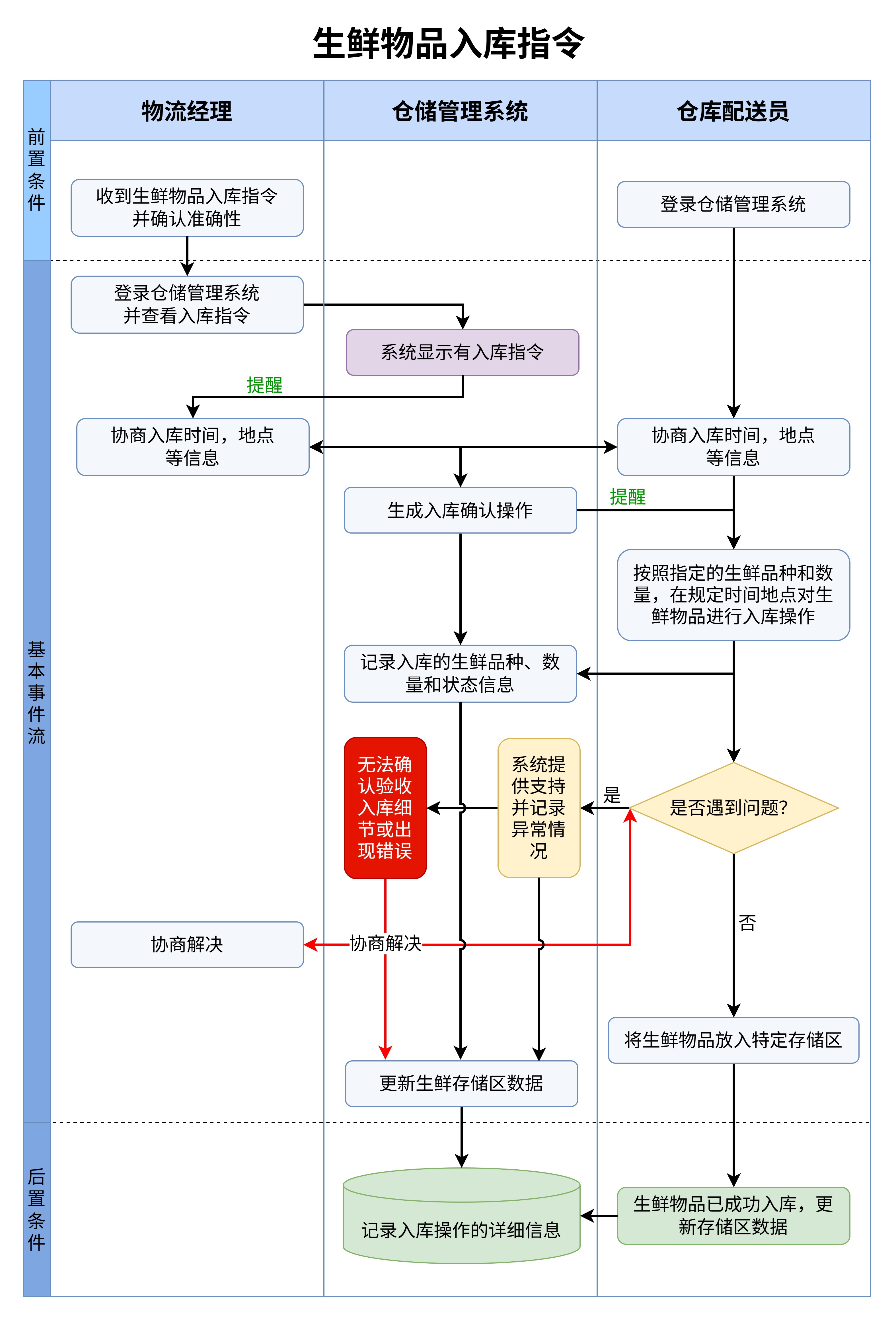
为了让大家更直观地理解5的阶乘计算过程，下面我们将通过一张流程图来展示这一过程。流程图不仅能帮助我们清晰地看到每个计算步骤，还能帮助我们更好地理解这些步骤之间的关系。

我们从5开始，接着计算5乘以4，得到的结果是20。然后再将20与3相乘，得到60。将60与2相乘，得到120。我们将120与1相乘，最终得到5的阶乘结果120。整个过程就是一个逐步累乘的过程，通过流程图展示出来，能够让我们对阶乘的计算过程有一个更加清晰的认识。

这就是计算5的阶乘的基本流程。通过这一简单的例子，我们不仅学习了阶乘的计算方法，还掌握了如何将计算过程可视化，进一步加深了对数学运算的理解。

程序实现5的阶乘

除了通过手动计算，我们还可以通过编程来实现5的阶乘。使用编程语言计算阶乘的方式有多种，其中最常见的两种方法是递归法和循环法。

1.递归法

递归是一种解决问题的思想，特别适用于阶乘的计算。我们可以定义一个递归函数来计算阶乘。在递归函数中，我们首先设置一个基本情况，即5!=5*4!，4!=4*3!，依此类推，直到计算到1!。代码如下所示：

deffactorial(n):

ifn==1:#基本情况

return1

else:

returnn*factorial(n-1)#递归调用

result=factorial(5)

print(result)#输出120

递归法的核心在于不断缩小问题的规模，直到问题可以简单地解决。这种方法虽然简洁，但在计算较大阶乘时，可能会导致栈溢出，因此需要特别注意递归深度的问题。

2.循环法

相比递归法，循环法更加直观且高效。我们通过一个循环，从1到n逐步累乘，从而得到阶乘值。下面是使用循环计算阶乘的Python代码：

deffactorial(n):

result=1

foriinrange(1,n+1):

result*=i

returnresult

result=factorial(5)

print(result)#输出120

循环法的优点在于它的效率较高，特别是对于计算较大阶乘时，它能避免递归带来的栈溢出问题。使用循环法，我们能够更加稳定和高效地计算出阶乘的结果。

阶乘的优化与扩展

尽管阶乘的计算方法看似简单，但在实际应用中，随着数字的增大，阶乘的计算量也会迅速增大。例如，20!的结果已经达到2,432,902,008,176,640,000，而更大的数字则更难计算。因此，阶乘的优化和扩展就显得尤为重要。

一种常见的优化方法是动态规划，通过存储已经计算过的阶乘值，避免重复计算，显著提高计算效率。比如，在计算20!时，我们可以先计算出10!，然后利用已计算出的结果继续计算后续的阶乘，减少不必要的重复计算。

还有一些特殊的优化方法，比如利用分治法将大的阶乘问题拆分为多个小问题并行计算，从而加速计算过程。这些优化方法在实际应用中，特别是处理大数据时，发挥了巨大的作用。

阶乘与其他数学概念的联系

阶乘不仅仅局限于计算一个数的乘积，它与其他许多数学概念有着密切的联系。比如，阶乘在排列组合中扮演着重要角色。在排列问题中，我们常常需要计算从n个不同物品中选出r个物品进行排列的数量，这时阶乘的计算就非常重要。排列组合中的公式往往都需要通过阶乘来进行推导和计算。

阶乘还与二项式定理、高斯积分等数学公式密切相关。在很多高级数学理论中，阶乘是不可或缺的工具。通过深入研究阶乘的性质，我们不仅能更好地理解这些数学公式，还能在实际应用中更高效地解决相关问题。

总结

计算5的阶乘虽然是一个简单的数学问题，但它所涉及的数学概念和算法思想却非常深刻。通过对5的阶乘计算过程的分析，我们不仅掌握了阶乘的定义和计算方法，还学会了如何将数学问题转化为程序代码进行计算。阶乘与其他数学概念的联系也使我们对它的重要性有了更深刻的认识。

无论是学习数学的同学，还是从事计算机科学工作的专业人士，阶乘的理解和运用都是必不可少的。通过本文的讲解，相信大家已经对阶乘有了更加清晰的理解，并能够将这一知识应用到实际的学习和工作中去。