拓扑图作为现代科学和技术领域中的重要工具,以其独特的方式揭示事物的内在联系与结构特征。本文将深入探讨拓扑图的基本概念、应用场景及其在不同领域的实际应用,帮助读者更好地理解这一复杂而优雅的数学工具。
拓扑图的起源可以追溯到18世纪的欧洲,由数学家欧拉在解决“七桥问题”时提出的。这一看似简单的问题实际上涉及到了图论中的一个重要概念——图的拓扑性质。拓扑图,简单来说,是一种用节点和边表示实体及其关系的数学模型。节点代表实体,边代表实体之间的连接或关联。这种抽象的表示方式使得拓assertFalse结构得以被清晰地分析和理解。
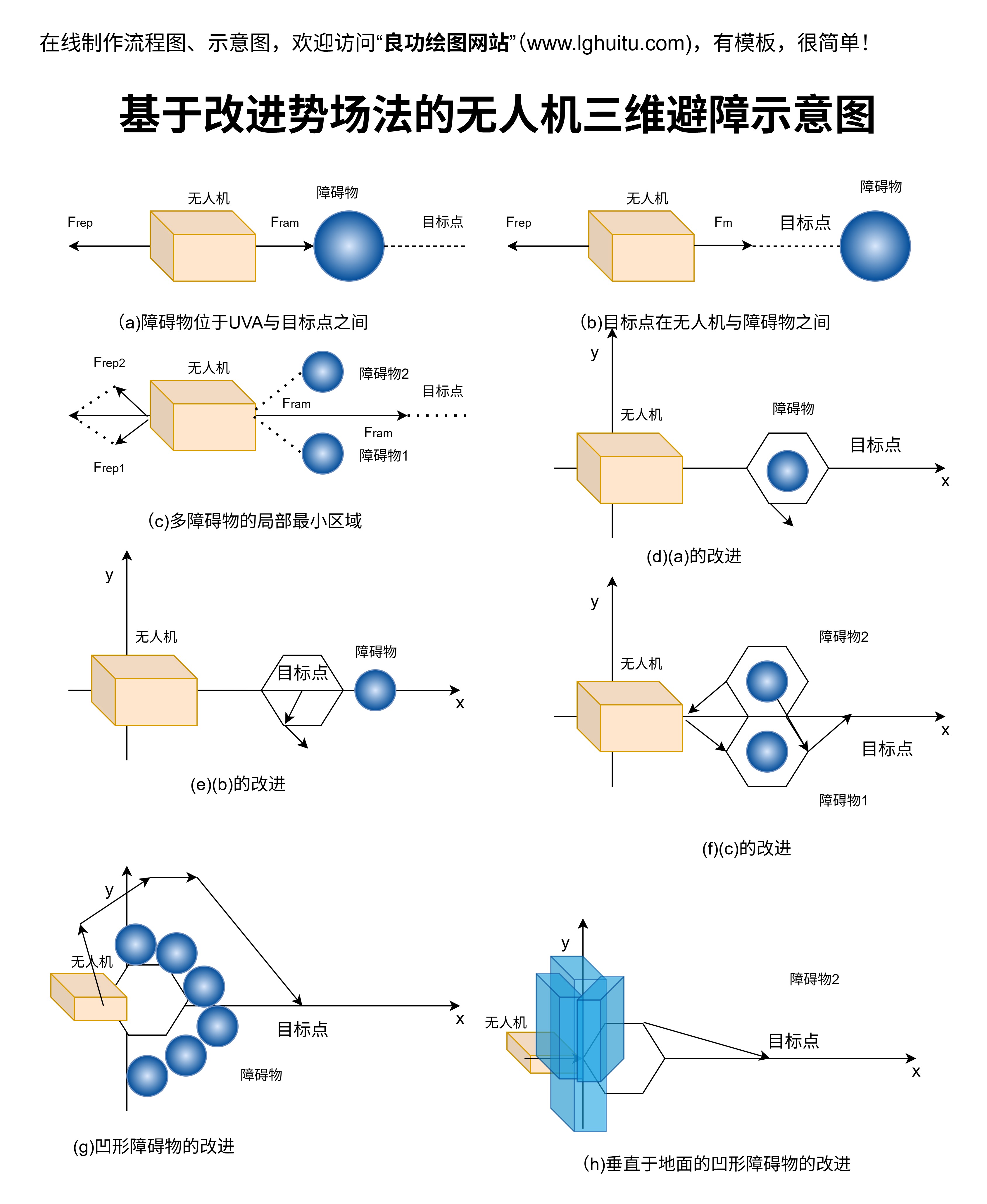
在拓扑图中,我们关注的是节点之间的连接方式及其相互关系,而不是具体的几何位置或物理距离。这种“去位置化”的特点使得拓扑图在处理复杂关系时具有独特的优势。例如,在社交网络分析中,拓扑图可以用来研究人与人之间的关系网络;在生物化学中,拓扑图则可用于分析蛋白质的相互作用网络。
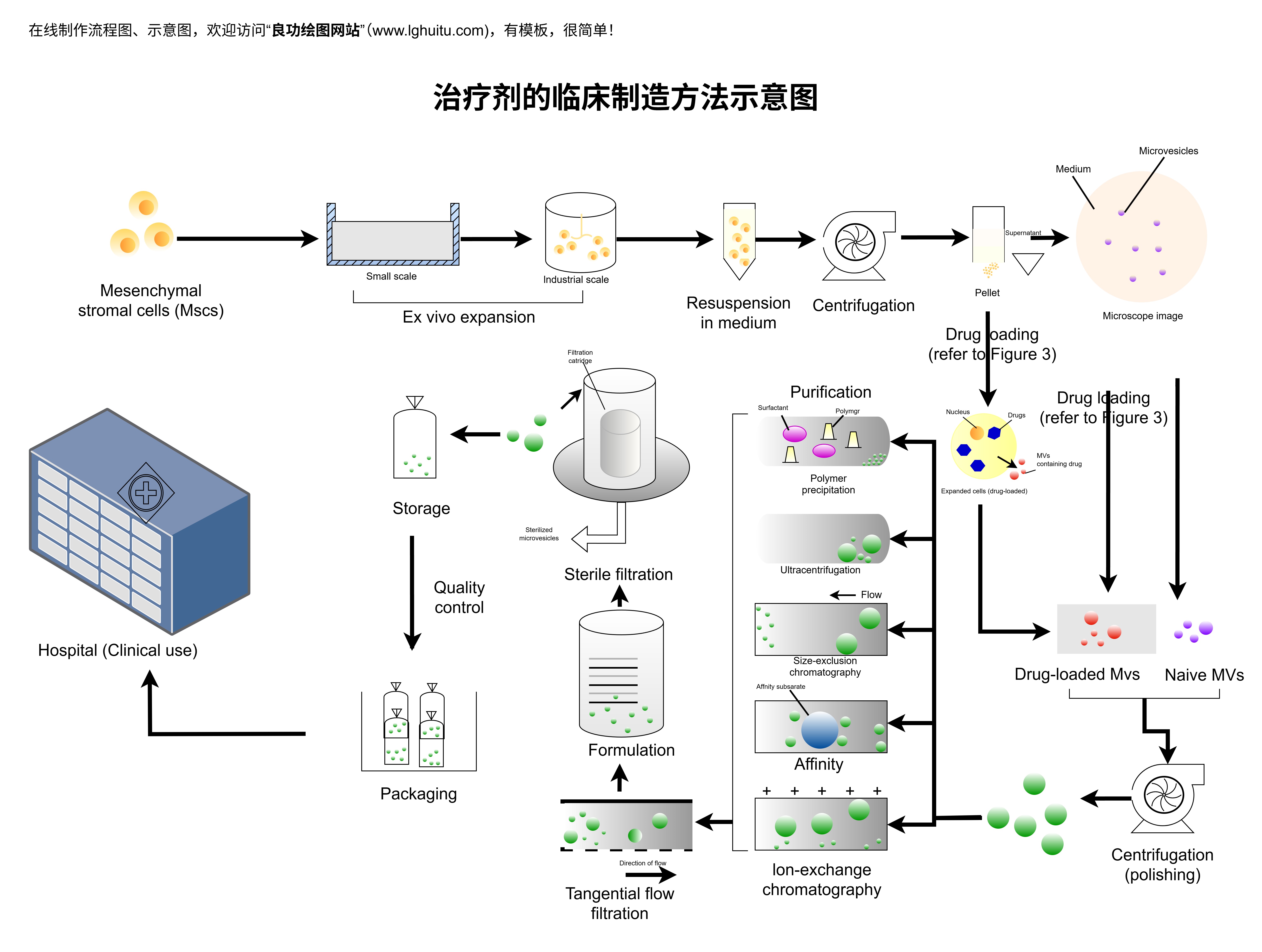
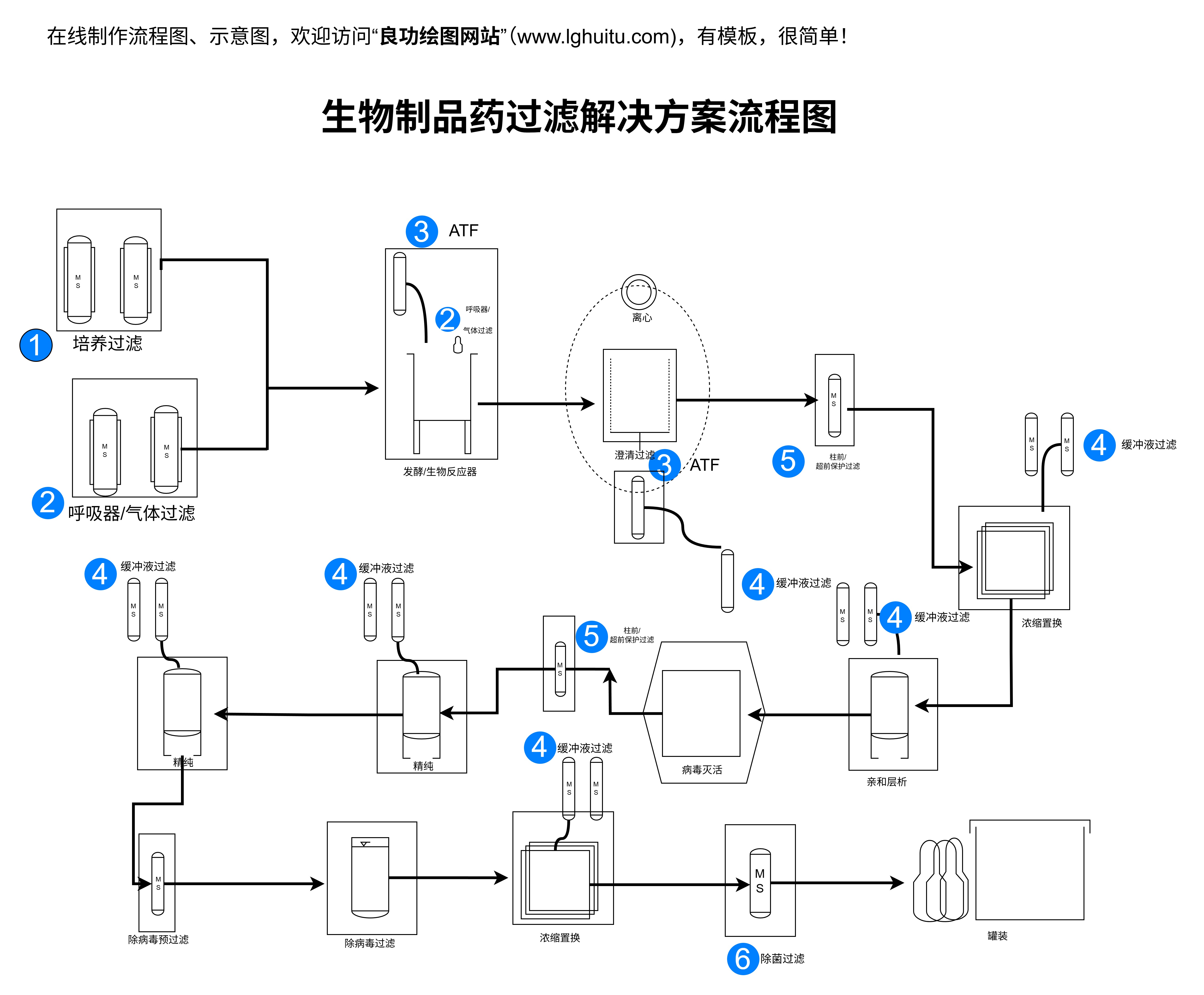
拓扑图的核心在于其能够将复杂的关系简化为直观的图形,从而帮助人们更好地识别模式、发现关键节点和优化系统结构。其在数据可视化、系统设计和网络分析等领域都发挥着重要作用。
拓扑图的应用场景极为广泛,几乎覆盖了我们生活的方方面面。以下将从几个关键领域详细探讨其应用价值。
在大数据时代,数据量的爆炸式增长使得传统的方法难以有效处理和分析数据。拓扑图通过其节点和边的结构,能够直观地展示数据之间的内在联系。例如,在金融领域,拓扑图可以用来分析股票市场的投资风险和资产间的关联性;在医疗领域,拓扑图则可用于研究疾病传播的网络模式。通过拓扑图,我们可以更清晰地识别关键节点(如高影响投资者或高传播疾病节点),从而为决策提供支持。
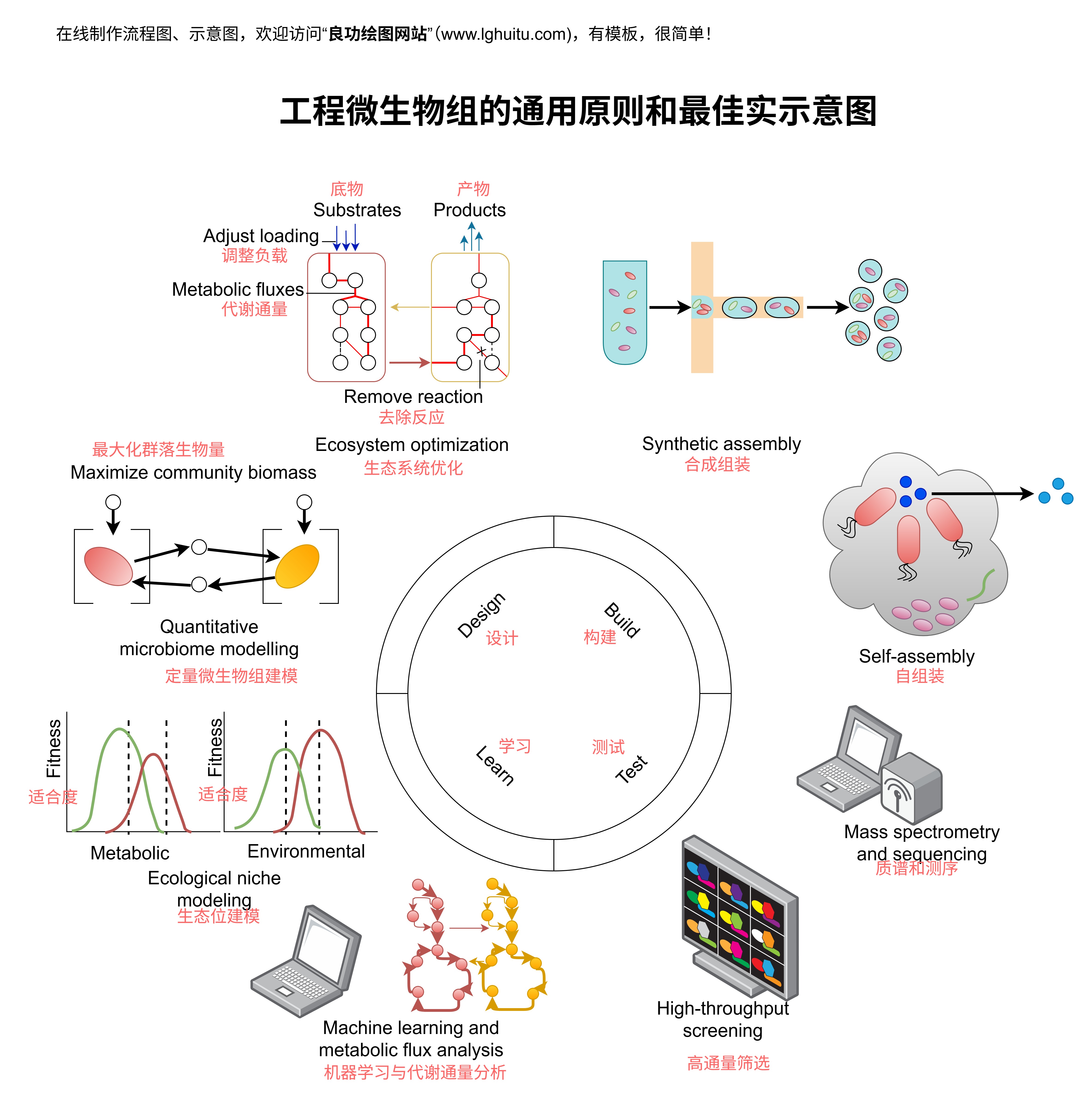
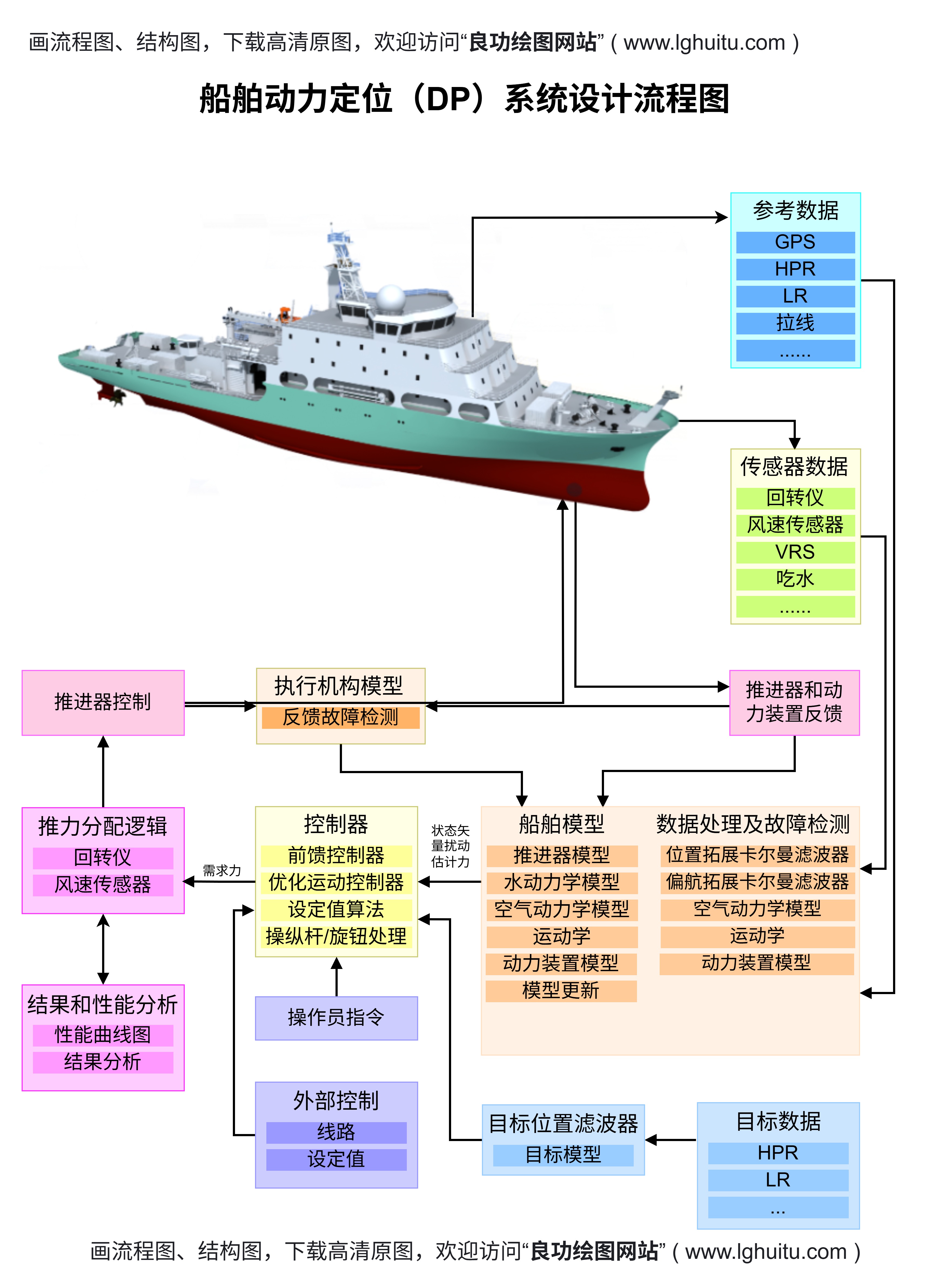
在计算机科学和网络工程中,拓扑图是系统设计和优化的重要工具。例如,在云计算中,拓扑图可以用来规划数据center的物理和虚拟机部署,以提高系统的效率和可靠性;在物联网领域,拓顶级图可以用来设计传感器网络的节点分布和数据传输路径。通过分析拓扑图的结构特性(如度分布、连通性、短路径等),我们可以优化系统性能,降低成本。
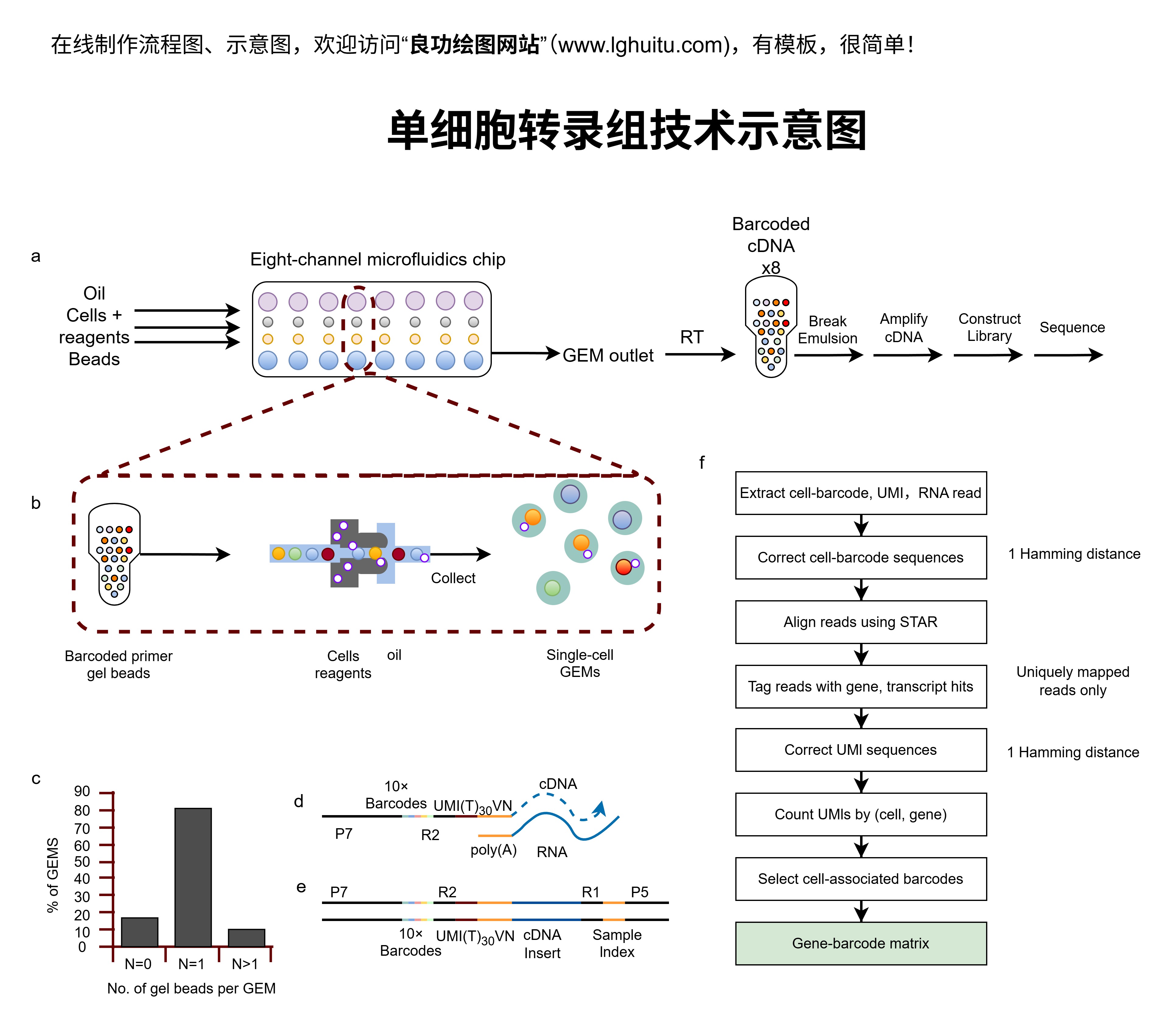
在城市规划和交通管理领域,拓扑图同样发挥着重要作用。例如,城市交通网络可以表示为拓扑图,其中节点代表交通信号灯、交叉路口或公交站点,边代表交通路线。通过分析拓扑图的特征,城市planners可以优化交通流量、减少拥堵,并提高城市交通效率。拓扑图还可以用于紧急情况下的疏散路线规划,确保在最坏情况下也能快速响应。
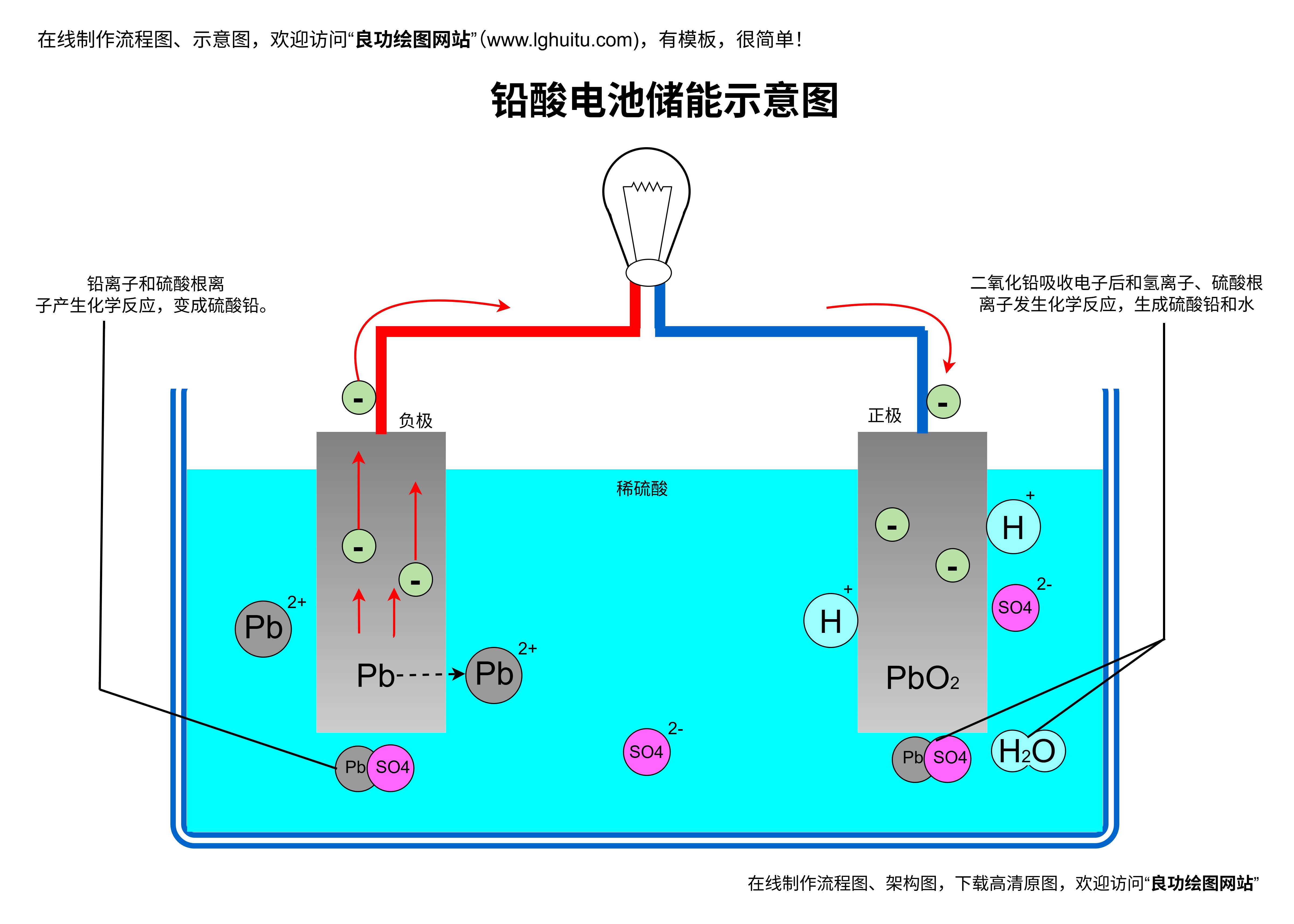
拓扑图在生物医学和化学研究中的应用尤为突出。例如,在蛋白质相互作用网络中,节点代表蛋白质分子,边代表蛋白质之间的相互作用。通过分析拓扑图的特性,研究人员可以识别关键蛋白质(如节点中心性高分子),从而为新药研发提供靶点。拓扑图还可以用于分析生物代谢网络,帮助揭示疾病机制并开发新型治疗方法。
在新能源领域,拓扑图同样具有重要的应用价值。例如,在风能和太阳能系统的布置中,拓扑图可以用来规划发电站的分布和能量传输路径,以最大化能量的捕获效率。拓扑图还可以用于分析可再生能源系统的稳定性,为系统的优化和扩展提供支持。
拓扑图作为现代科学和技术领域中的重要工具,以其独特的抽象能力与分析视角,为复杂系统和关系提供了简洁而直观的表示方式。无论是在数据科学、计算机科学,还是在城市规划、生物医学等领域,拓拓扑图的应用都为人类社会的优化与发展提供了强大的技术支持。未来,随着人工智能和大数据技术的进一步发展,拓扑图的应用将更加广泛,其重要性也将得到更加充分的体现。